Les contraintes représentent les efforts de cohésion dans un solide qui permettent à la matière à résister aux sollicitations.
Les contraintes sont issues d'interaction entre des petites parties de la matière (cristaux, molecules ... etc ...).
L'équivalent de la contrainte pour un fluide parfait est la pression.
Soit un corps ![]() sollicité par un ensemble d'actions mécaniques
et en équilibre dans un référentiel. Toute partie de
sollicité par un ensemble d'actions mécaniques
et en équilibre dans un référentiel. Toute partie de ![]() est en équilibre.
est en équilibre.

Si on coupe ![]() par un plan cd mormale
par un plan cd mormale
![]() passant par le point P, les deux parties
passant par le point P, les deux parties ![]() située
du côté de la normale et
située
du côté de la normale et ![]() située du côté opposé,
sont en équilibre.
située du côté opposé,
sont en équilibre.

![]() est en équilibre sous l'effet:
est en équilibre sous l'effet:
Le vecteur contrainte est homogène à un effort par unité de surface ou une pression, il s'exprime en Pascals.
Il existe aussi des unités plus exotiques:
L'emploi de ces unités est vivement déconseillé.
Si en un point P on effectue deux plans de coupure de normales
![]() et
et
![]() , on obtient deux vecteurs contraintes
, on obtient deux vecteurs contraintes
![]() et
et
![]() qui sont à priori différents.
qui sont à priori différents.
En deux points P et Q d'un même plan de coupure de normale
![]() on obtient deux vecteurs contraintes
on obtient deux vecteurs contraintes
![]() et
et
![]() qui sont à priori différents.
qui sont à priori différents.
Le torseur résultant des actions de ![]() sur
sur ![]() pour
un plan de coupure
pour
un plan de coupure ![]() de normale
de normale
![]() est
:
est
:
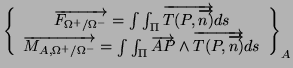
Le vecteur contrainte se décompose en une contrainte normale ![]() et une contrainte tangentielle
et une contrainte tangentielle
![]()
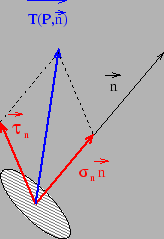
On peut écrire:
![]()
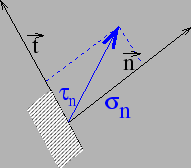
![]()
Dans ce cas les contraintes normales et tangentielles sont des nombres.
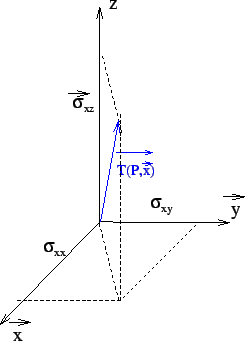
Soit
![]() une base (orthonormée directe tant qu'à faire), on nomme les projections
des vecteurs contraintes de la manière suivante:
une base (orthonormée directe tant qu'à faire), on nomme les projections
des vecteurs contraintes de la manière suivante:
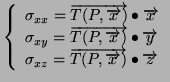
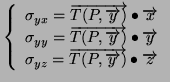
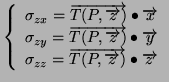
Soit
![]() , l'application définie
au point P qui à une normale
, l'application définie
au point P qui à une normale
![]() associe
le vecteur des contraintes
associe
le vecteur des contraintes
![]() .
.
![]()