1. Poutre hyperstatique

Une poutre de longueur L, d’inertie par rapport à l’axe Gz : I_gz, est encastrée à son extrémité O et est simplement posé à son extrémité B ; une charge répartie s’exerce sur toute sa longueur (figure 2).

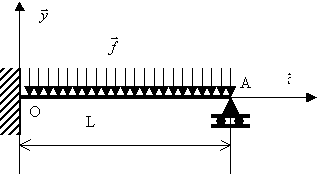
Figure 1

On décide de décomposer le problème en deux problèmes isostatiques.

1.1 Problème isostatique N° 1 :

L’encastrement en 0 est remplacé par un appui simple, le chargement est identique au chargement initial (figure 3).

Figure 2

Calculer:

ü Les efforts de cohésion (tracer les diagrammes correspondants).

ü L’équation de la déformée.

ü La rotation w₀₁ au point O

1.2 Problème isostatique N° 2 :

L’encastrement en 0 est remplacé par un appui simple, le chargement est remplacé par un moment ponctuel (figure 4).

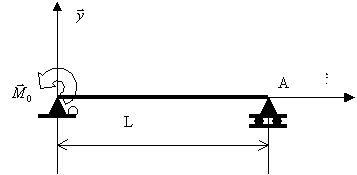
Figure 3

Calculer:

ü Les efforts de cohésion (tracer les diagrammes correspondants).

ü L’équation de la déformée.

ü La rotation w₀₂ au point O

1.3 Problème hyperstatique :

La solution du problème hyperstatique est la somme des solutions des deux problèmes précédents lorsque est tel que la rotation soit nulle.

ü Calculer M₀ en fonction de f pour que w₀ = w₀₁ + w₀₂ = 0

ü Tracer les diagrammes du moment fléchissant et de l’effort tranchant du problème total.

ü Calculer la flèche.