Next: 2 Poutre continue: Up: Correction du contôle de Previous: Correction du contôle de

Subsections

1.1 Résolution des problèmes isotatiques
1.2 Calcul de l'inconnue hyperstatique
1.3 Calcul des réactions d'appui:
1.4 Calcul des sollicitations:

1 Poutre encastrée appuyée:

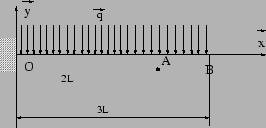
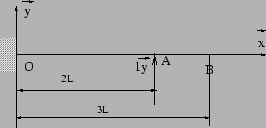
Le problème hyperstatique d'ordre 1, se décompose en deux problèmes isostatiques P_b0 et $P_{b1}=Y_{A}\overline{P_{b1}}$ .

1.1 Résolution des problèmes isotatiques

On calcule pour chaque problème:

Le moment fléchissant.
Les variables demandées pour le problème hyperstatique soit: Les réactions d'appui, l'effort tranchant.

Attention aux notations: M_o:moment d'encastrement au point O, M₀ : Moment pour le problème P_b0.

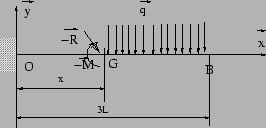
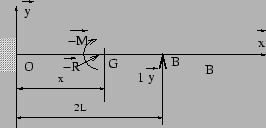
On choisit la décomposition suivante:

Problème 0 Problème $\overline{1}$

$\resizebox*{0.48\textwidth}{!}{\includegraphics{pb0.eps}}$ $\resizebox*{0.48\textwidth}{!}{\includegraphics{pb1.eps}}$

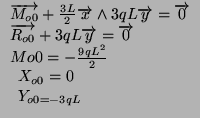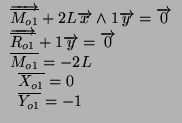$\begin{array}{l} \overrightarrow{M_{o0}}+\frac{3L}{2}\overrightarrow{x}\wedge... ...qL^{2}}{2}\\ \begin{array}{l} X_{o0}=0\\ Y_{o0=-3qL} \end{array}\end{array}$ $\begin{array}{l} \overrightarrow{\overline{M_{o1}}}+2L\overrightarrow{x}\wedg... ...{array}{l} \overline{X_{o1}}=0\\ \overline{Y_{o1}}=-1 \end{array}\end{array}$

$\resizebox*{0.48\textwidth}{!}{\includegraphics{pb0_mom.eps}}$ $\resizebox*{0.48\textwidth}{!}{\includegraphics{pb1_mom.eps}}$

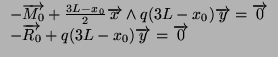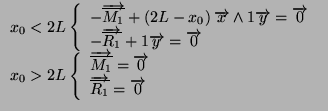$\begin{array}{l} -\overrightarrow{M_{0}}+\frac{3L-x_{0}}{2}\overrightarrow{x}... ...ightarrow{R_{0}}+q(3L-x_{0})\overrightarrow{y}=\overrightarrow{0} \end{array}$ $\begin{array}{l} x_{0}<2L\left\{ \begin{array}{l} -\overrightarrow{\overline{... ...ghtarrow{\overline{R_{1}}}=\overrightarrow{0} \end{array}\right. \end{array}$

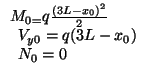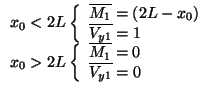$\begin{array}{l} M_{0=}q\frac{(3L-x_{0})^{2}}{2}\\ \begin{array}{l} V_{y0}=q(3L-x_{0})\\ N_{0}=0 \end{array}\end{array}$ $\begin{array}{l} x_{0}<2L\left\{ \begin{array}{l} \overline{M_{1}}=\left( 2L-... ...{l} \overline{M_{1}}=0\\ \overline{V_{y1}}=0 \end{array}\right. \end{array}$

$\overline{N_{1}}=0$

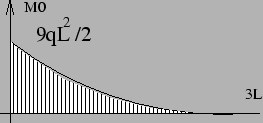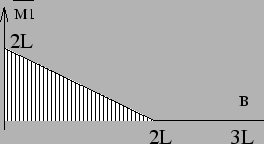$\resizebox*{0.48\textwidth}{!}{\includegraphics{diagm0.eps}}$ $\resizebox*{0.48\textwidth}{!}{\includegraphics{diagm1.eps}}$

1.2 Calcul de l'inconnue hyperstatique

L'inconnue hyperstatique est donc:

$\begin{displaymath} Y_{A}=-\frac{\int ^{3L}_{0}M_{0}\overline{M_{1}}}{\int ^{3L}_{0}\overline{M_{1}}\overline{M_{1}}}\end{displaymath}$

On ne peut pas simplement trouver $\int ^{3L}_{0}M_{0}\overline{M_{1}}$ car les longueurs des abscisses des diagrammes (3L pour M₀ et 2L pour $\overline{M_{1}}$ )ne correspondent pas, il faut faire le calcul à la main.

$\int ^{3L}_{0}M_{0}\overline{M_{1}}=\int ^{2L}_{0}q\frac{(3L-x_{0})^{2}}{2}\left( 2L-x_{0}\right) dx_{0}=\frac{17qL^{4}}{3}$

Par contre le calcul de $\int ^{3L}_{0}\overline{M_{1}}\overline{M_{1}}$ se fait facilement en utilisant les intégrales de Mohr (Attention la longueur de l'abscisse est 2L)

$\int ^{3L}_{0}\overline{M_{1}}\overline{M_{1}}=\frac{8L^{3}}{3}$

On en déduit:

$\begin{displaymath} Y_{A}=-\frac{17qL}{8}\end{displaymath}$

1.3 Calcul des réactions d'appui:

$M_{o}=M_{o0}+Y_{A}\overline{M_{o1}}$ soit $M_{o}=-3q\frac{L^{2}}{2}+\frac{17qL}{8}2L=\frac{11qL^{2}}{4}$

$Y_{o}=Y_{o0}+Y_{A}\overline{Y_{o1}}$ soit : $Y_{o}=-3qL+\frac{17qL}{8}=-\frac{7qL}{8}$

1.4 Calcul des sollicitations:

x₀<2L :

$V_{y}=V_{y0}+Y_{A}\overline{V_{y1}}=q(3L-x_{0})-\frac{17qL}{8}$

$M=M_{0}+Y_{A}\overline{M_{1}}=q\frac{(3L-x_{0})^{2}}{2}-\frac{17qL}{8}\left( 2L-x_{0}\right)$

$V_{y}=q\left( \frac{7L}{8}-x_{0}\right)$ et $V_{y}\left( 0\right) =\frac{7qL}{8}$ , $V_{y}\left( 2L\right) =-\frac{11qL}{8}$ , $V_{y}\left( \frac{7L}{8}\right) =0$

$M\left( 0\right) =\frac{qL^{2}}{4}$ , $M\left( \frac{7L}{8}\right) =\frac{-17qL^{2}}{128}$ et $M\left( 2L\right) =\frac{qL^{2}}{2}$

x₀>2L :

$V_{y}=V_{y0}+Y_{A}\overline{V_{y1}}=V_{y0}=q(3L-x_{0})$

$M=M_{0}+Y_{A}\overline{M_{1}}=q\frac{(3L-x_{0})^{2}}{2}$

$V_{y}\left( 2L\right) =qL$ et $V_{y}\left( 3L\right) =0$

$M\left( 2L\right) =\frac{qL^{2}}{2}$ et $M\left( 3L\right) =0$

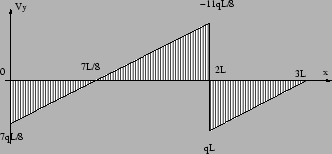
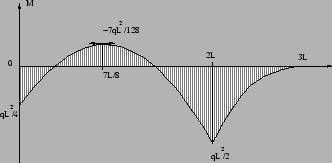
On peut maintenant tracer les diagrammes. Il sont tracés dans l'hypothèse où q<0:

$\resizebox*{0.6\textwidth}{!}{\includegraphics{diagVy.eps}}$

$\resizebox*{0.6\textwidth}{!}{\includegraphics{diagMf.eps}}$

Next: 2 Poutre continue: Up: Correction du contôle de Previous: Correction du contôle de

La Borderie 2002-09-20

Problème 0	Problème $\overline{1}$
$\resizebox*{0.48\textwidth}{!}{\includegraphics{pb0.eps}}$	$\resizebox*{0.48\textwidth}{!}{\includegraphics{pb1.eps}}$
$\begin{array}{l} \overrightarrow{M_{o0}}+\frac{3L}{2}\overrightarrow{x}\wedge... ...qL^{2}}{2}\\ \begin{array}{l} X_{o0}=0\\ Y_{o0=-3qL} \end{array}\end{array}$	$\begin{array}{l} \overrightarrow{\overline{M_{o1}}}+2L\overrightarrow{x}\wedg... ...{array}{l} \overline{X_{o1}}=0\\ \overline{Y_{o1}}=-1 \end{array}\end{array}$
$\resizebox*{0.48\textwidth}{!}{\includegraphics{pb0_mom.eps}}$	$\resizebox*{0.48\textwidth}{!}{\includegraphics{pb1_mom.eps}}$
$\begin{array}{l} -\overrightarrow{M_{0}}+\frac{3L-x_{0}}{2}\overrightarrow{x}... ...ightarrow{R_{0}}+q(3L-x_{0})\overrightarrow{y}=\overrightarrow{0} \end{array}$	$\begin{array}{l} x_{0}<2L\left\{ \begin{array}{l} -\overrightarrow{\overline{... ...ghtarrow{\overline{R_{1}}}=\overrightarrow{0} \end{array}\right. \end{array}$
$\begin{array}{l} M_{0=}q\frac{(3L-x_{0})^{2}}{2}\\ \begin{array}{l} V_{y0}=q(3L-x_{0})\\ N_{0}=0 \end{array}\end{array}$	$\begin{array}{l} x_{0}<2L\left\{ \begin{array}{l} \overline{M_{1}}=\left( 2L-... ...{l} \overline{M_{1}}=0\\ \overline{V_{y1}}=0 \end{array}\right. \end{array}$
	$\overline{N_{1}}=0$
$\resizebox*{0.48\textwidth}{!}{\includegraphics{diagm0.eps}}$	$\resizebox*{0.48\textwidth}{!}{\includegraphics{diagm1.eps}}$