Next: About this document ... Up: Correction du contôle de Previous: 1 Poutre encastrée appuyée:

Subsections

2.1 Calcul des moments isostatiques $M_{0}\protect$ dans chaque travée:
2.2 Application de la formule des trois moments:
- En $C_{1}:\protect$
- En $C_{2}:\protect$
2.3 Résolution:
2.4 Diagramme des moments fléchissants:

2 Poutre continue:

2.1 Calcul des moments isostatiques $M_{0}\protect$ dans chaque travée:

Travée 1:

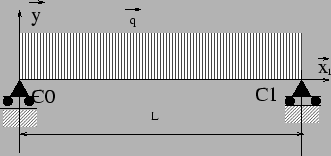
$\resizebox*{0.6\textwidth}{!}{\includegraphics{poutcont_pbO.eps}}$

$\begin{displaymath} M_{0}=-\frac{qx\left( L-x\right) }{2}\end{displaymath}$

$\resizebox*{0.6\textwidth}{!}{\includegraphics{poutcont_m1.eps}}$

Travée2

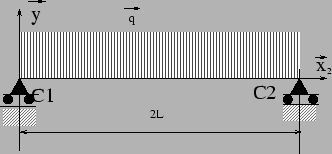
$\resizebox*{0.6\textwidth}{!}{\includegraphics{poutcont_pb2.eps}}$

$\begin{displaymath} M_{0}=-\frac{qx\left( 2L-x\right) }{2}\end{displaymath}$

$\resizebox*{0.6\textwidth}{!}{\includegraphics{poutcont_m2.eps}}$

Travée 3:

On peut considérer la travée entière, mais il faudra ensuite faire attention que le moments fléchissant dü à l'inconnue hyperstatique X₂ est nul sur la partie de la poutre en porte à faux.

On peut aussi considérer une travée réduite à sa portion entre les appuis C₂ et C₃ en imposant le moment qL²/2 appliqué par la partie de poutre en porte à faux sur la portion considérée en C₃.

Quelque soit l'option choisie, le problème reste hyperstatique d'ordre 2 et la formule des trois moments ne peut être appliquée que 2 fois.

$\resizebox*{0.6\textwidth}{!}{\includegraphics{poutcont_pb3.eps}}$

$\begin{displaymath} x<L\quad :\quad M_{0}=\frac{qx^{2}}{2}\end{displaymath}$

$\begin{displaymath} x>L\quad :\quad M_{0}=\frac{q\left( 2L-x\right) ^{2}}{2}\end{displaymath}$

$\resizebox*{0.6\textwidth}{!}{\includegraphics{poutcont_m3.eps}}$

2.2 Application de la formule des trois moments:

En $C_{1}:\protect$

$2X_{1}\left( 3L\right) +X_{2}\left( 2L\right) +6\int _{\Gamma _{1}}M_{0}\frac{x_{1}}{L}dx_{1}+6\int _{\Gamma 2}M_{0}\frac{2L-x_{2}}{2L}dx_{2}=0$

Les intégrales sont facilement obtenues :

$6\int _{\Gamma _{1}}M_{0}\frac{x_{1}}{L}dx_{1}=-\frac{qL^{3}}{4}$ et $6\int _{\Gamma 2}M_{0}\frac{2L-x_{2}}{2L}dx_{2}=-2qL^{3}$

et donc:

$6LX_{1}+2LX_{2}=\frac{qL^{3}}{4}+2qL^{3}$

24X₁+8X₂=9qL²

(1)

En $C_{2}:\protect$

$X_{1}(2L)+2X_{2}\left( 3L\right) +6\int _{\Gamma 2}M_{0}\frac{x_{2}}{2L}dx_{2}+6\int _{\Gamma 3}M_{0}\frac{L-x_{3}}{L}dx_{3}=0$

Attention sur la troisième travée : $\Gamma _{3}$ se limite ici à la zone d'intervention du moment hyperstatique X₃, c'est à dire sur la première partie de la travée. Le moment fléchissant provoqué par X₃ sur la partie de la travée en porte à faux est nul.

Les intégrales sont facilement obtenues :

$6\int _{\Gamma 2}M_{0}\frac{x_{2}}{2L}dx_{2}=-2qL^{3}$ et $6\int _{\Gamma 3}M_{0}\frac{L-x_{3}}{L}dx_{3}=\frac{qL^{3}}{4}$

et donc:

$2LX_{1}+6LX_{2}=2qL^{3}-\frac{qL^{3}}{4}$

2.3 Résolution:

8X₁+24X₂=7qL²

(2)

3*(1)-(2) $\Rightarrow$ : 64X₁=20qL² soit : $X_{1}=\frac{5qL^{2}}{16}=-700kN$

3*(2)-(1) $\Rightarrow$ : 64X₂=12qL² soit : $X_{2}=\frac{3qL^{2}}{16}=-420kN$

2.4 Diagramme des moments fléchissants:

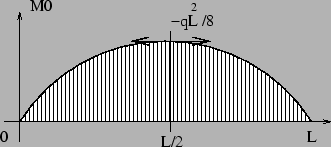
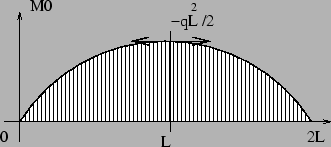
Le diagramme de l'effort tranchant n'étant pas demandé, on étudie directement les moments fléchissants et les extréma sont obtenus par dérivarion.

Sur la première travée:

$M=M_{0}+X1\frac{x_{1}}{L}$ soit $M=-\frac{qx_{1}\left( L-x_{1}\right) }{2}+\frac{5qL}{16}x_{1}=\frac{q}{16}x_{1}\left( 5L-8L+8x_{1}\right)$

$\begin{displaymath} M=\frac{q}{16}x_{1}\left( 8x_{1}-3L\right) \end{displaymath}$

$\frac{dM}{dx_{1}}=\frac{q}{16}\left[ \left( 8x_{1}-3L\right) +8x_{1}\right] =q\left( x_{1}-\frac{3L}{16}\right)$

$M\left( 0\right) =0$ , $M\left( L\right) =X1=\frac{5qL^{2}}{16}$ , $M\left( \frac{3L}{8}\right) =0$ et $M\left( \frac{3L}{16}\right) =-\frac{9qL^{2}}{512}=39,375kN$

Sur la deuxième travée:

$M=M_{0}+X1\frac{2L-x_{2}}{2L}+X_{2}\frac{x_{2}}{2L}$ soit

$M=-\frac{qx_{2}\left( 2L-x_{2}\right) }{2}+\frac{5qL}{16}\frac{2L-x_{2}}{2}+\... ...}\frac{x_{2}}{2}=\frac{qx^{2}_{2}}{2}-\frac{17qLx_{2}}{16}+\frac{5qL^{2}}{16}$

$\begin{displaymath} M=\frac{q}{16}\left( 8x^{2}_{2}-17Lx_{2}+5L^{2}\right) \end{displaymath}$

$\frac{dM}{dx_{2}}=\frac{q}{16}\left( 16x_{2}-17L\right)$

$M\left( 0\right) =X_{1}=\frac{5qL^{2}}{16}$ , $M\left( 2L\right) =X_{2}=\frac{3qL^{2}}{16}$ , et

$M\left( \frac{17L}{16}\right) =-\frac{129qL^{2}}{512}=564,375kN$

Sur la troisième travée:

Pour x₃<L

$M=M_{0}+X_{2}\frac{x_{3}}{L}$ soit $M=\frac{qx^{2}_{3}}{2}+\frac{3qL}{16}\left( L-x_{3}\right) =\frac{q}{16}\left( 8x^{2}_{3}-3Lx_{3}+3L^{2}\right)$

$\begin{displaymath} \frac{q}{16}\left( 8x^{2}_{3}-3Lx_{3}+3L^{2}\right) \end{displaymath}$

$\frac{dM}{dx_{3}}=\frac{q}{16}\left( 16x_{3}-3\right) =q\left( x_{3}-\frac{3L}{16}\right)$

$M\left( 0\right) =X_{2}=\frac{3qL^{2}}{16}$ , $M\left( L\right) =\frac{qL^{2}}{2}$ , et

$M\left( \frac{3L}{16}\right) =\frac{87qL^{2}}{512}=-380,625kN$

$\resizebox*{1\textwidth}{!}{\includegraphics{poutcontmom.eps}}$

Next: About this document ... Up: Correction du contôle de Previous: 1 Poutre encastrée appuyée:

La Borderie 2002-09-20